NystromBestiary-v1.zip [17.3Mb] contains the code, a copy of the "Revisiting" paper, and the datasets used in the paper. It is released under the Creative Commons Attribution 3.0 Unported License.
Webpages of the authors: Alex Gittens and Michael Mahoney.
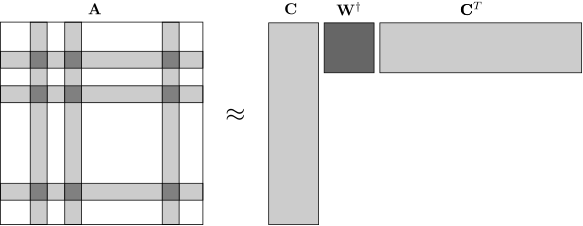
Nystrom extensions are a class of low-rank approximations for symmetric positive-semidefinite matrices, inspired by an eponymously named technique used by numerical analysts. The most basic such approximation consists of sampling columns uniformly at random (with or without replacement) from the matrix \(\mathbf{A}\) to form the matrix \(\mathbf{C}\) and taking the approximation to be \(\mathbf{C} \mathbf{W}^\dagger \mathbf{C}^T\), where \(\mathbf{W}^\dagger\) is the pseudoinverse of the matrix \(\mathbf{W}\) comprising the overlap of \(\mathbf{C}\) and \(\mathbf{C^T}\).

The attraction of this particular approximation is that it can be formed much quicker than a low-rank approximation based on the eigendecomposition, and is often almost as accurate. When this approximation is not appropriate, one can mix the columns of \(\mathbf{A}\) before forming the extension, giving rise to a large class of possible extensions. These are more costly to compute (although still less so than using the eigendecomposition), but have more theoretical guarantees.
Accordingly, one is interested in theoretical bounds on the quantities \(\|\mathbf{A} - \mathbf{C}\mathbf{W}^\dagger \mathbf{C}^T\|_\xi\), where \(\xi\) denotes the spectral, Frobenius, or trace norm, and \(\mathbf{C}\) is generated from \(\mathbf{A}\) using some combination of mixing and column-sampling. Such bounds are given in Revisiting the Nystrom Method for Improved Large-Scale Machine Learning; optimality of some of these bounds are established in Revisiting the Nystrom Method for Improved Large-Scale Machine Learning. and On The Lower Bounds of The Nystrom Method.
Of course, there is a gap between optimal worse-case bounds and what is observed in practice, so empirical error and timing information is crucial to developing an understanding of the practical benefits and limitations of Nystrom extensions. The Nystrom Bestiary is a collection of Matlab code that implements Nystrom extensions and provides an interface for computing and visualizing their errors and timing information. It was used to produce the figures in the paper Revisiting the Nystrom Method for Improved Large-Scale Machine Learning, where the lessons learned from these empirical investigations are discussed at length. We release it here in the spirit of reproducible research.